CogSci Lounge

I had often been asked "What kind of model is yours?" referring to my thesis work. I have always felt puzzled while attempting to answer that question - my model is/was neither a "linear mixed model", "graphical model", "drift diffusion model", or anything I could put a label on. I'd have called it a "mechanistic model", but the puzzling look on the faces remained.

In the back of my mind, I have heard the terms "causal models", "mechanistic models", "statistical models". But I have a hard time explaining the exact differences between each of them - all of them come with equations, so you cannot simply use the absence or presence of them to eliminate.

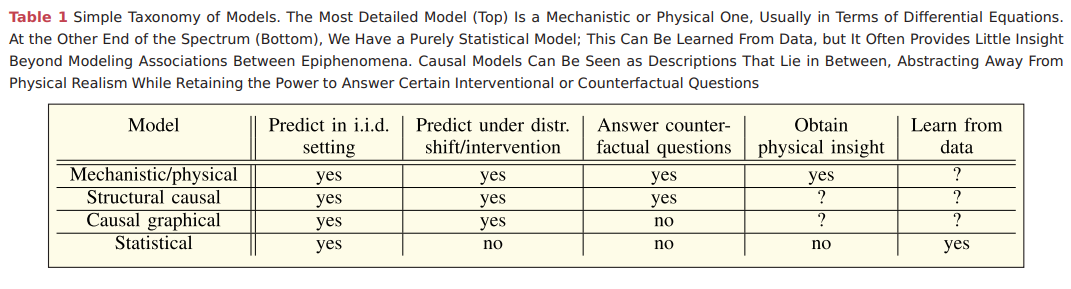
I recently found the below table in a paper on Towards Causal Representational Learning, which might explain some differences and be of interest to some people.

I am not sure what the situation is in other countries, but atleast in India, it seems that the standard math syllabus until class 10 or even 12 is insufficient for developing a good intuition for functions and their graphs, or graphs and their functions. So, this post is an attempt to collect resources to help develop that intuition.

First up is a video lecture series by Aaron Schkoler: https://www.youtube.com/playlist?list=PL57pneHQXdPYtFmmxeRWN9WPZyc9oc2q8

Second up is a slightly advanced (but still basic) booklet by University of Sydney's Mathematics Learning Center: https://www.sydney.edu.au/content/dam/students/documents/mathematics-learning-centre/functions-and-graphs.pdf. This contains exercises and also solutions. Be sure to do the exercises - math is like cycling, you cannot just learn math by listening and reading if you do not do it yourself.

You can also augment the above resources with a graphing app like Grapher. Use it frequently, play with it, engage with it.

This one isn't free, but it seems like an excellent read.

http://bayes.cs.ucla.edu/BOOK-2K/

In the Preface to the Second Edition, J. P. writes:

My main audience remain the students: students of statistics who wonder why instructors are reluctant to discuss causality in class; students of epidemiology who wonder why elementary concepts such as confounding are so hard to define mathematically; students of economics and social science who question the meaning of the parameters they estimate; and, naturally, students of artificial intelligence and cognitive science, who write programs and theories for knowledge discovery, causal explanations, and causal speech.